Waves and Sound for the MCAT: Everything You Need to Know
/Learn key MCAT concepts about waves and sound, plus practice questions and answers
(Note: This guide is part of our MCAT Physics series.)
Part 1: Introduction to waves and sound
Part 2: Characteristics of periodic motion
a) Amplitude
b) Frequency
c) Phase
Part 3: Sound
a) Transverse and longitudinal waves
b) Sound production
c) Sound intensity
Part 4: Wave phenomena
a) Doppler effect
b) Shockwaves
c) Resonance
Part 5: High-yield terms
Part 6: Practice equations
Part 7: Passage-based questions and answers
Part 8: Standalone questions and answers
----
Part 1: Introduction to waves and sound
Periodic motion is an important concept that shows up in a wide range of topics. Conceptually, periodic motion occurs as a result of many common forces and potentials. Mathematically, it presents a great opportunity to practice wave graphs, which are incredibly powerful and versatile tools of analysis. Graphical depiction of periodic motion is identical to that of sound, which is itself a slightly different example of a wave. Mastering these concepts will help you understand many basic systems as well as waves and their characteristics.
On the MCAT, periodic motion and sound are medium-yield topics. Similar to our other guides, the most important terms below are in bold font. When you see one, try to define it in your own words and use it to create your own examples. This is a great way to check your understanding, and phrasing things in a way that makes the most sense to you will make studying much easier (and much more effective!) in the long run.
At the end of this guide, you’ll also find several practice problems for you to hone your knowledge. Let’s begin!
----
Part 2: Characteristics of periodic motion
Periodic motion is any motion that repeats itself. Common examples are pendulums, bobbing springs, and skateboarders going up and down a halfpipe. Graphs are especially helpful when working with periodic motion, because it’s easy to see the repeating patterns when they are represented visually. The most natural shape for periodic motion is a sine wave, but it’s possible to see other shapes as well, including triangle waves, square waves, or completely irregular waves.
When graphing periodic motion, displacement is usually on the y-axis and time is on the x-axis.
Figure: Examples of periodic waves
There are three values that define periodic motion: its amplitude, frequency, and phase. Any regular form of periodic motion can be defined through these three variables only. We’ll discuss each in further detail.
a) Amplitude
If something is undergoing periodic motion, its amplitude is its maximum displacement from rest (or displacement=0). For example, imagine a weight hanging from a spring. Starting from rest, the weight can be pulled down to initiate a bobbing motion. The amplitude would be the distance from the weight’s highest point to the middle point.
Figure: Amplitude of a sine wave.
This middle point, or when displacement is equal to zero, is often called the object’s equilibrium position. On a graph, the amplitude describes the height of the peaks and the depths of the troughs. Amplitude is always given in units of a displacement. This means meters when the displacement is a distance, or radians or degrees when the displacement is an angle.
b) Frequency
On a graph, you can qualitatively describe the frequency by how dense the peaks are. Waves that appear to be denser have higher frequencies. However, it’s important to check that the time scale on each x-axis is represented on the same scale!
FIgURE: Wave 1 has higher frequency than wave 2.
To calculate the frequency from a graph, first measure the period of oscillation: the length of one complete cycle, by measuring from one peak to another. The period is the reciprocal of frequency (or P=1/f), so you can find the frequency simply by dividing 1 by the measured period.
Figure: Frequency is the reciprocal of the period.
You can also use the frequency and wavelength to determine the velocity of a wave.
$$v=f\times \lambda$$ $$\mbox{where } v \mbox{ = velocity of the wave,}$$ $$f \mbox{ = frequency,}$$ $$\lambda \mbox{ = wavelength}$$
The angular frequency is how many radians are passed through in one second. To convert linear frequency to angular frequency, multiply by 2π. This is because there are 2π radians per rotation.
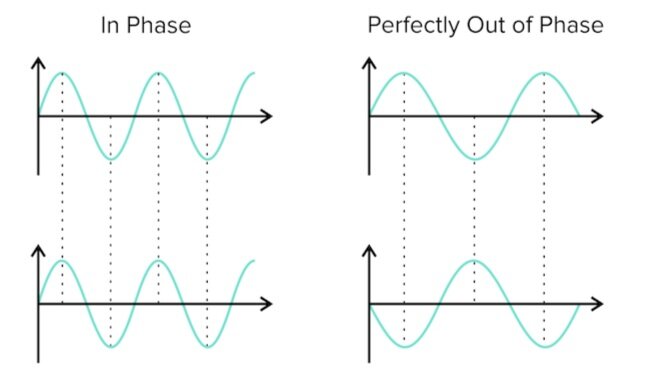
c) Phase
Phase refers to the relationship between two different waves. Two waves are in phase if their maxima and minima occur at the same points in time. When adding waves that are in phase with one another, they will constructively interfere: their maxima will add to become an even greeted maximum, and so will minima. The equilibrium position should remain the same.
Waves are out of phase if their peaks do not line up exactly and are perfectly out of phase if the peaks of one wave occur at the same time as the troughs of the other. When waves get more and more out of phase, they interfere more destructively. When waves are perfectly out of phase, two waves of the same magnitude will cancel each other out completely and sum to a wave of zero amplitude.
Figure: Waves In phase and perfectly out of phase.
To try and visualize this, imagine a system made of one spring attached to a wall and a system made of two other identical springs also attached to a wall. Pressing a block 1 cm into the one-spring system will cause the block to slide back and forth with an amplitude of 1 cm.
In the two-block system:
The oscillation of the springs will be in phase if you press a block into the springs such that both are compressed 1 cm. They will interfere constructively, and the total amplitude of the block’s motion will be 2 cm.
The springs will be out of phase if you compress one 1 cm and compress the other 1 cm after releasing the block (sounds hard to do in real life, but we can still think about it!). The total amplitude of the block’s motion will be less than 2 cm.
The springs will be perfectly out of phase if you compress one 1 cm and stretch the other 1 cm. The total amplitude of the block’s motion will be 0 cm.
Note that waves can be in and out of phase if they have different amplitudes. Phase differences will tell you how to add them.
Gain instant access to the most digestible and comprehensive MCAT content resources available. 60+ guides covering every content area. Subscribe today to lock in the current investments, which will be increasing in the future for new subscribers.