Electrostatics, Magnetism, and Circuits for the MCAT: Everything You Need to Know
/Learn key MCAT concepts about electrostatics, magnetism, and circuits, plus practice questions and answers
(Note: This guide is part of our MCAT Physics series.)
Table of Contents
Part 1: Introduction to electrostatics, magnetism, and circuits
Part 2: Electrostatics
a) Charge
b) Conservation of charge
c) Coulomb’s Law
d) Electric field
e) Electric potential
Part 3: Circuits
a) Voltage and electromotive force
b) Current
c) Resistance
d) Ohm’s law
e) Capacitors
Part 4: Magnetism
a) Lorentz force
b) Magnetic field and current
Part 5: High-yield terms and equations
Part 6: Passage-based questions and answers
Part 7: Standalone questions and answers
-----
Part 1: Introduction to electrostatics, magnetism, and circuits
Electricity and magnetism (E&M) is a field of physics that describes interactions between charged particles. The topics covered here can be a little daunting because, unlike mechanics, E&M describes phenomena that are less readily observable in everyday life. Nevertheless, with the help of analogies and visualizations, even this topic can become intuitive.
On the MCAT, electrostatics, magnetism, and circuits are considered to be medium-yield topics. While you may not be tested directly on these topics, they will be important in the context of neurological circuits and instrument design.
Several key terms in this guide are listed in bold font. Try to define these terms in your own words and create your examples. Phrasing things in a way that makes the most sense to you will make studying much easier (and much more effective!) in the long run. At the end of this guide, there are also several practice questions to test your understanding.
Let’s begin!
-----
Part 2: Electrostatics
Electrostatics is the study of electromagnetic phenomena at equilibrium—that is, systems in which there are no moving charged particles. This is in contrast to the study of electromagnetism in circuits, which consists of moving charged particles.
a) Charge
The most fundamental quantity in electrostatics and magnetism is charge. Charge is a physical property of matter that causes the particle to experience a force in an electric field.
It may be helpful to compare the concept of a particle’s charge to the concept of an object’s mass: just as mass is the amount of matter that is subject to gravitational fields, charge represents a quantity within a particle that is subject to electric fields.
Charge comes from protons and electrons. Charge is a scalar, and it is measured in units of Coulombs (C).
All charge is made of combinations of protons and electrons. Protons and electrons are elementary charges, which means they are the smallest possible units of charge. The magnitude of their charge is 1.6 x 10-19 coulombs. In the case of protons, this value is positive; for electrons, this value is negative. (Neutrons, the third building block of atoms, have no charge.)
b) Conservation of charge
When the charge of an object changes, it does so because some number of protons or electrons move to another object. No protons or electrons are created or destroyed but instead are relocated to another place. This principle is called the conservation of charge.
Consider a conductor that has no net charge. After creating a charge on it (more on this later), either end of the conductor will gain or lose charge to create a positive or negative pole. However, since charge is conserved, the net charge of the entire conductor will remain zero.
Figure: Charge is conserved, even when poles gain negative or positive charges.
c) Coulomb’s Law
Recall that opposite charges attract, and like charges repel. Formally, this rule is stated by Coulomb’s law:
$$F = -\frac{kq_1q_2}{r^2}$$ $$\mbox{where }F\mbox{ = the force exerted between the charges,}$$ $$k \mbox{ = Coulomb's constant=} 8.98\times 10^9,$$ $$q_1, q_2\mbox{ = the two charges,}$$ $$r\mbox{ = the distance between the two charges}$$
Coulomb’s law provides us a vector representing the amount of attractive force between two charged particles. As with all vectors, we must keep the direction in mind. There are a few methods to do this.
A simple method to do so is to plug in the magnitudes of each particle and decide the direction at the end of the problem. With two particles, this is as easy as remembering that the force should attract opposite charges together and repel like charges apart.
A slightly more difficult method is to keep track of the direction the whole time. Coulomb’s law states the force on just one of the charges, such as q1. Then r has to be the distance from q1 to q2. If you imagine the charges on the x-axis, r will either be positive (point rightwards) or negative (point leftwards).
Remember the negative in front of the whole equation and the different charges. If the charges are opposite, their product will be negative and will “cancel” with the negative sign in front. If they are the same sign, their product will be positive and will not cancel. If the negative sign in the front of the equation is canceled out, the force on q1 will point in the same direction as the arrow from q1 to q2. In other words, it is attractive. If the negative sign remains, the force will point in the opposite direction. In other words, it is repulsive.
Figure: The signs of the charges determine whether the force points in the same direction as the distance vector connecting them.
Figure: Coulomb's law can be applied to systems with multiple charges.
d) Electric field
An electric field is a region in which a charge will feel a force. The equation for the force experienced by a charge in an electric field is very simple:
$$F = E\times q$$ $$\mbox{where }F\mbox{ = the force exerted on the charge,}$$ $$E \mbox{ = the electric field,}$$ $$q \mbox{ = the value of the charge}$$
Notice that the electric field is a vector, and therefore has positive or negative directions. Thus, positive charges will experience a force in the same direction as the electric field, and negative charges will experience forces in the opposite direction.
Electric field is given in units of newtons per coulomb (N/C), or volts per meter (V/m).
Field lines are used to graphically represent electric fields. We represent an electric field as a collection of straight arrows. The relative strength of an electric field is given by the density of the arrows. (The same is true for all vector fields.)
Figure: Field lines for uniform electric fields.
When comparing Coulomb’s law and the force on charge in an electric field, you might notice that the equations would be the same if : $$E=-\frac{kq_1}{r^2}$$ This is because the value $$-\frac{kq_1}{r^2}$$ represents the electric field created by charges. So, Coulomb’s law is actually just a specific case of a force due to an electric field.
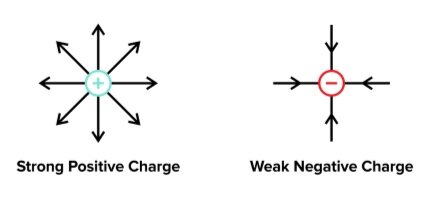
Positive charges create fields that point outward, and negative charges create fields that point inward.
Figure: Field lines due to single point charges.
The fields generated by individual point charges will interact with each other in a predictable manner.
Figure: Field lines generated by two charges.
Gain instant access to the most digestible and comprehensive MCAT content resources available. 60+ guides covering every content area. Subscribe today to lock in the current investments, which will be increasing in the future for new subscribers.