Atomic and Molecular Structure for the DAT
/Learn key DAT concepts about atomic and molecular structure, plus practice questions and answers
Everything you need to know about atomic and molecular structure for the DAt
Table of Contents
Part 1: Introduction to atomic and molecular structure
Part 2: Electronic structure of atoms
a) Atomic structure
b) Electron configuration
c) Electron spin
d) Quantum mechanical model
e) Electron cloud model
Part 3: Molecular structure
a) Ionic bonds
b) Covalent bonds
c) Coordinate covalent bonds
d) Single and double bonds
Part 4: High-yield terms
Part 5: Questions and answers
----
Part 1: Introduction to atomic and molecular structure
Atoms and molecules make up the basic units of matter, and are the basis of many general chemistry concepts. This guide will teach you everything you need to know about atomic and molecular structure for the DAT. Pay attention to the high-yield, bolded terms, and test yourself with DAT-style practice questions and answers at the end.
----
Part 2: Electronic structure of atoms
a) Atomic structure
Atoms are composed of three primary subatomic particles: protons, neutrons, and electrons. A proton carries a positive charge of +1e, where "e" signifies the fundamental unit of charge and is equivalent to one atomic mass unit (AMU). Conversely, neutrons have no charge and possess a mass of one AMU. Protons and neutrons, collectively referred to as nucleons, congregate within the nucleus of an atom.
Meanwhile, electrons bear a negative charge of -1e and exhibit a mass approximately 1/1823th of a proton or neutron. Essentially, when comparing the masses of electrons to protons or neutrons, the electron's mass is deemed negligible. Electrons are organized into shells encircling the atom, with those in the outermost shell termed valence electrons. Valence electrons are pivotal in chemical reactions and bond formation
| Subatomic particle | Charge | Mass |
|---|---|---|
0 AMU |
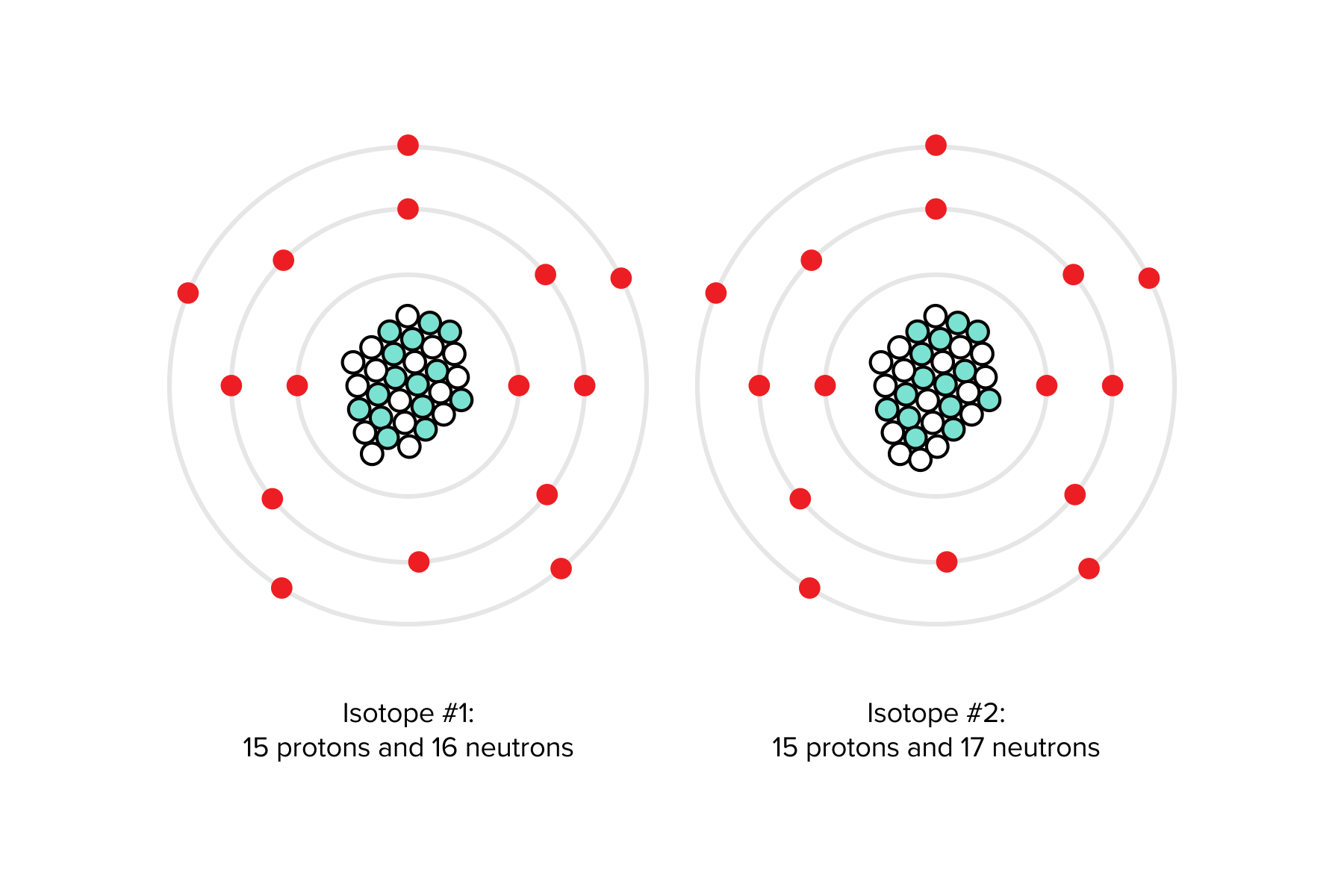
It's important to recognize that an atom's identity is determined by the number of protons it contains. This characteristic, known as the atomic number, uniquely defines the element to which the atom belongs. For instance, any atom with 15 protons is classified as phosphorus, regardless of the number of neutrons present.
Atoms sharing the same atomic number but differing numbers of neutrons are referred to as isotopes. For example, various isotopes of phosphorus may have 16 or 17 neutrons alongside 15 protons. Despite these differences in neutron count, all isotopes of phosphorus retain the same atomic number, identifying them as phosphorus variants.
FIGURE 1: TWO ISOTOPES OF PHOSPHORUS
As a result, two isotopes of an element will possess differing atomic mass: a measure of mass that is calculated by summing the number of protons and neutrons within an atom. The atomic mass of many isotopes is used to calculate atomic weight, which is a weighted average of masses of all naturally occurring isotopes.
For an elemental isotope that is represented by \({}^A_ZX\) (where X is the element), the following properties can be determined:
- Atomic number (Z): the number of protons in an atom, which determines the elemental identity of the isotope (e.g., any isotopes with 15 protons must be phosphorus)
- Mass number (A): the number of protons and neutrons in an atom (e.g., 30P contains 15 protons and 15 neutrons, resulting in an atomic mass of 30)
- Atomic weight: the weighted average of the masses of naturally occurring isotopes (e.g., if half of all naturally occurring isotopes are 30P and the remaining half is 31P, the atomic weight would be the average of the two mass numbers multiplied by their abundance. Since both isotopes are equally abundant, the atomic weight is 30.5 AMU.)
How is it possible that numerous protons, each carrying a positive charge, remain tightly bound within the nucleus? Given that similar charges repel, you might expect the positive charges of the protons to drive the nucleus apart. However, the strong nuclear force serves as the pivotal factor preventing this scenario. This fundamental force acts as an attractive binding force, effectively holding protons and neutrons together within the nucleus, despite their mutual positive charges.
b) Electron configuration
The arrangement of subatomic particles within an atom is a fundamental aspect of atomic structure. At the nucleus, protons and neutrons are bound together by the strong nuclear force, forming the central core of the atom. However, the organization of electrons outside the nucleus is considerably more intricate.
Electron configurations serve as a conventional method for describing the arrangement of electrons within an atom. Essentially, an electron configuration provides a sort of "address" for an element, detailing the distribution of its electrons across different energy levels. For instance, the electron configuration of phosphorus is denoted as [Ne]3s2 3p3.
Determining an electron configuration involves identifying the number of electrons present in the given species. For most atoms, which are electrically neutral, the number of electrons corresponds to the atomic number of the element. This equivalence arises from the fact that electrons carry negative charges, while protons possess positive charges, resulting in overall neutrality. However, for ions—particles with a net positive or negative charge—the number of electrons may differ from the atomic number.
When filling the electron shells of an atom, electrons occupy concentric regions surrounding the nucleus. Although these "shells" are not tangible structures, they serve as a useful conceptual framework for understanding electron distribution. The number of concentric shells is determined by the atom's group number in the periodic table. Elements in the first row have one electron shell, those in the second row possess two, and so on. Generally, shells with higher numbers are situated farther from the nucleus, with the outermost shell, known as the valence shell, located at the greatest distance.
Valence electrons refer to the electrons occupying the outermost shell of an atom, dictating its reactivity and distinct properties. An atom achieves its maximum energetic stability when its valence shell is complete with electrons. Notably, certain elements, such as noble gases, possess a fully occupied valence shell, rendering them particularly stable.
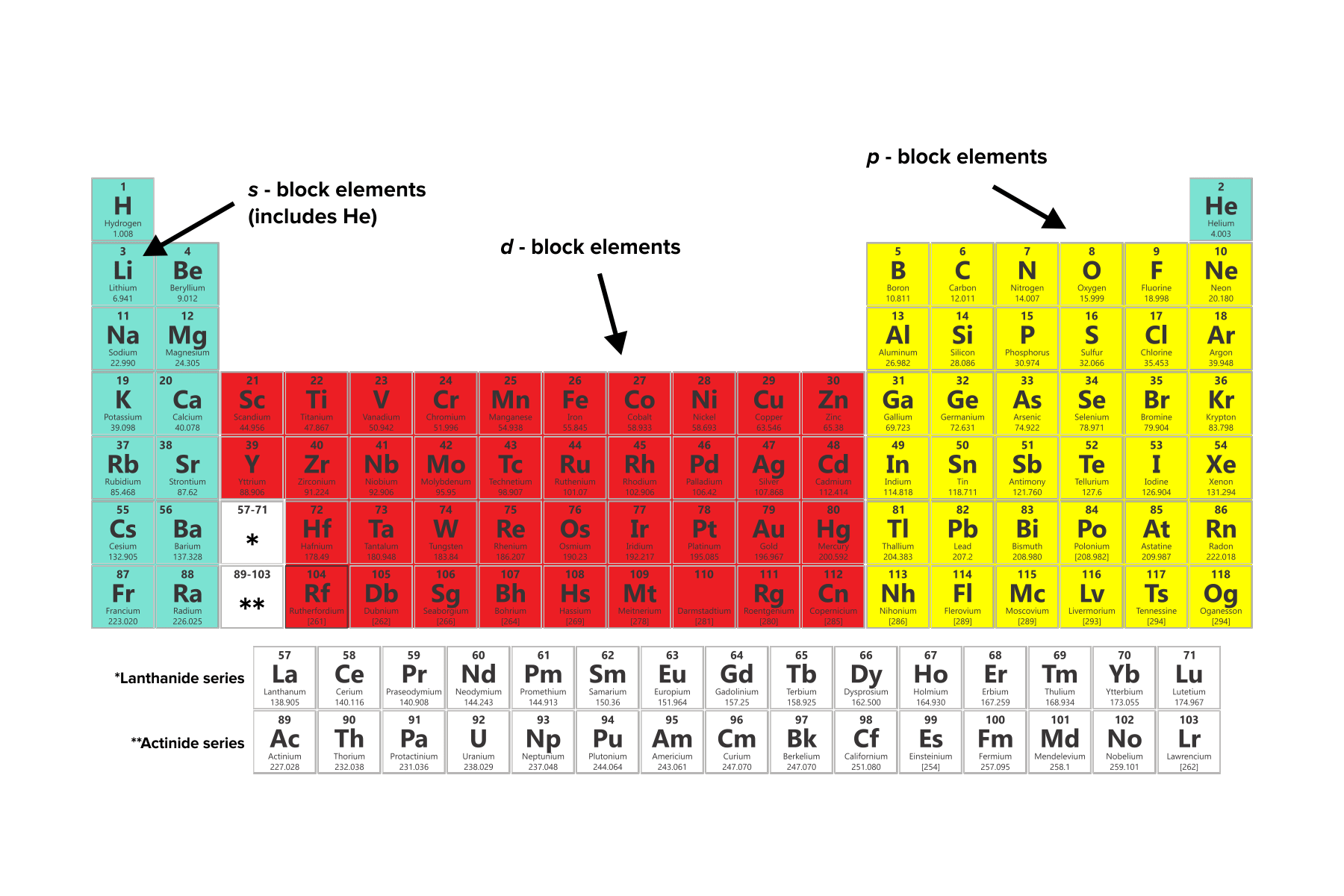
Each shell consists of orbitals, distinct regions of specific shapes where electrons are most likely to be found. While various orbital shapes exist, the DAT emphasizes three primary types: s, p, and d orbitals. Elements are classified into different blocks—s-block, p-block, and d-block—based on the highest-energy orbital they contain. There is one s orbital, three p orbitals, and five d orbitals.
FIGURE 2: ELEMENTS CATEGORIZED BY OUTERMOST VALENCE ELECTRON ORBITALS
Grouping elements according to their highest-energy orbital generally aligns with their elemental characteristics. The majority of s-block and d-block elements are categorized as metals, while p-block elements encompass a combination of metalloids and nonmetals.
To determine the electron configuration of a neutral atom, do the following:
1. Identify the group number of the atom by locating its position on the periodic table. For instance, halogens belong to the seventeenth group or column of the periodic table.
FIGURE 3: ELEMENTS IN THE SEVENTH GROUP
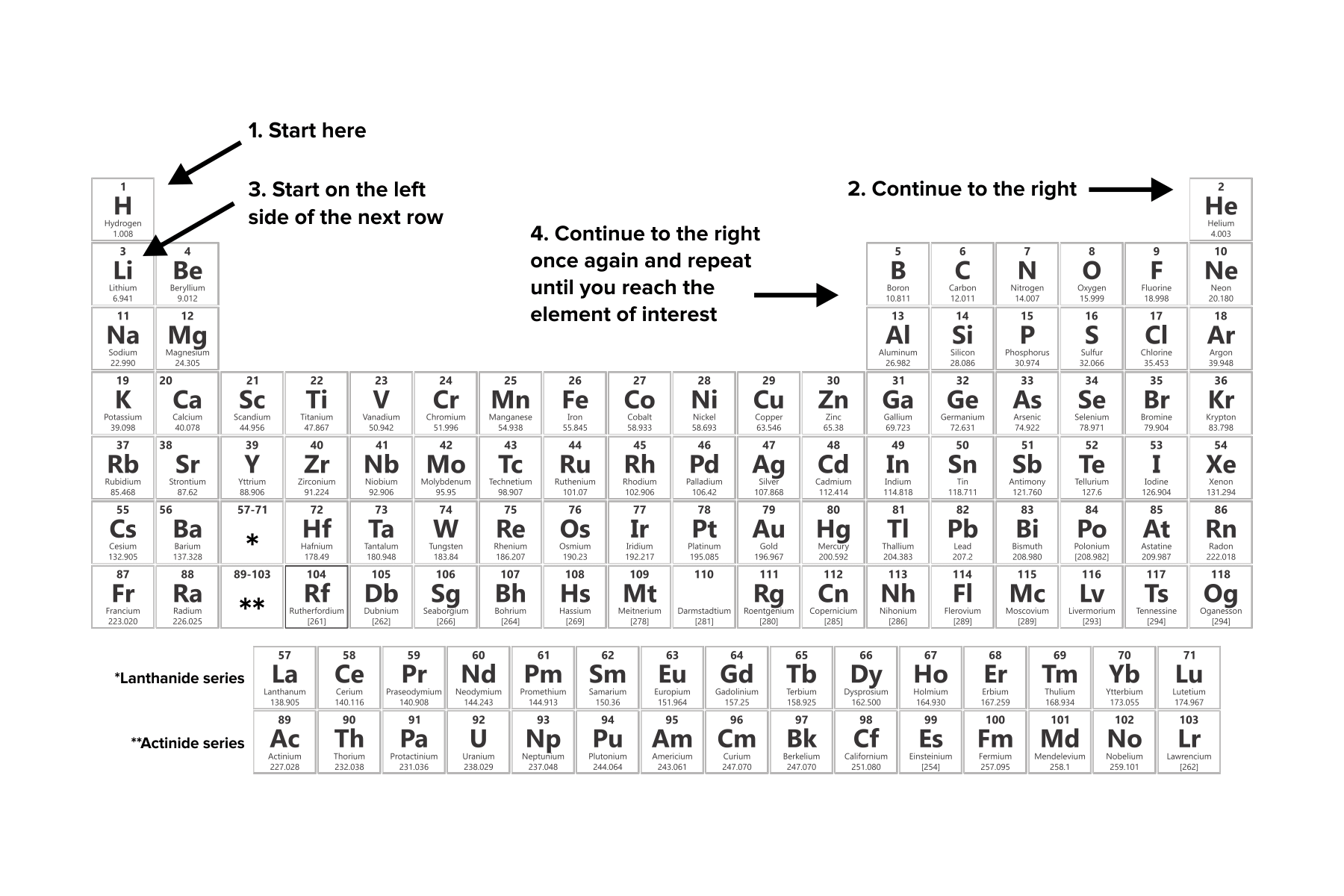
2. Familiarize yourself with the sequence of electron filling within shells. Electrons occupy shells in a predetermined order that follows these guidelines:
Electron occupation begins with the first "subshell" or orbital, starting with hydrogen's orbital.
Successive electron occupation proceeds to the right across the periodic table. Once a row or family is fully occupied, filling resumes with the leftmost element of the subsequent row.
According to the Aufbau principle, each orbital within a shell must be filled sequentially before electrons can occupy the next available shell.
Electron filling ceases once the appropriate number of electrons is distributed among the orbitals. For atoms with neutral charges, this electron count matches the atomic number of the element.
FIGURE 4: GUIDELINES FOR FILLING ELECTRON CONFIGURATIONS.
Consider the electron configuration of lithium (Li).
- Electrons are always placed in lower energy shells first, so we begin at the top left of the periodic table with the 1s orbital.
- For every increase in the group number, we have an additional electron to account for. Thus, the electron configuration of hydrogen is 1s1, and helium is 1s2.
- After filling the first row, move to row 2. Lithium is 1s22s1.
Electron configurations can also be written using noble gas configuration. This is a shorthand form for electron configuration, in which writing the electron configuration begins at the closest preceding noble gas. Thus, the electron configuration of lithium can also be written as [He]2s1. Filling of the s and p orbitals is fairly straightforward. The d-block elements, or metals, require slightly more consideration. Let’s consider the electron configuration of iron (Fe).
- Using noble gas configuration, we can start with the identity of the closest preceding noble gas: [Ar].
- Iron is located in group number 8. Thus, we must fill in 8 electrons.
- Using the path of electron filling, the 4s2 must be filled first using two electrons.
- Six electrons must be placed in the next orbital. While in the first three rows, the s-block filling was followed by p-block filling, the fourth-row elements also contain a d-orbital. Perhaps confusingly, these are of a lower shell number.
- Thus, the six electrons are placed in the 3d6.
- The electron configuration for Fe is [Ar]4s23d6.
c) Electron spin
Electrons have a property known as spin, which can be either up or down. In the 1s orbital, there are two electrons, and each must have an opposite spin. In larger orbitals, such as p or d orbitals, Hund's rule dictates that each orbital is initially occupied by one electron before any orbital gets a second electron. Additionally, these single electrons will all have the same spin.
FIGURE 5: AN APPLICATION OF HUND’S RULE IN FILLING ORBITALS WITH ELECTRONS. NOTE THAT EACH 2P ORBITAL IS FILLED WITH SINGLE ELECTRONS OF THE SAME SPIN BEFORE ELECTRONS ARE PAIRED TOGETHER.
The balance between spin-up and spin-down electrons influences an element's magnetic properties. Atoms with all electrons paired (each pair consisting of one spin-up and one spin-down electron) are diamagnetic and do not interact strongly with magnets. Conversely, paramagnetic atoms have unpaired electrons, meaning they have more spin-up electrons than spin-down electrons. Paramagnetic materials are significantly affected by nearby magnetic fields but do not have a permanent magnetic charge.
FIGURE 6: HELIUM IS DIAMAGNETIC, WHILE LITHIUM IS PARAMAGNETIC
Ferromagnetic materials are a type of paramagnetic material with an extra feature: the spins of unpaired electrons can spontaneously align in the same direction. This alignment causes the ferromagnetic material to generate its own magnetic field. Most common magnetic items, like refrigerator magnets, are made of ferromagnetic materials.
d) Quantum mechanical model
The quantum mechanical model of atoms describes an electron in an atom using four quantum numbers: n, l, ml, and ms. Why is this system important?
Consider building a coffee table with hundreds of screws. Each screw serves the same purpose—holding the table together—but no two screws can occupy the same position simultaneously. This principle mirrors the Pauli exclusion principle, which states that no two electrons can have the same four quantum numbers. If asked to describe a single screw in the table, you could talk about its length, orientation, and 3D position, but it would be complex and lengthy. Imagine having a simple system to describe the placement of these screws.
Although we lack a simplified system for describing screw positions in a coffee table, the quantum mechanical model effectively describes the position and orbit of electrons in an atom using four quantum numbers:
| Quantum number | Range | Notes |
|---|---|---|
Determines the type of orbital ℓ = 0 → s orbital ℓ = 1 → p orbital ℓ = 2 → d orbital |
||
Determines the spin orientation of an electron +1/2 → spin up -1/2 → spin down |
Let’s apply this system to naming an electron: in this instance, the one and only electron that a neutral hydrogen atom possesses. In this case:
- n=1, as the hydrogen atom is located in the first row of the periodic table and thus has one electron shell
- l=0, as the electron must fill an s orbital
- ml=0
- ms=+1/2, as spin up electrons are filled before spin down electrons
e) Electron cloud model
How are electrons spatially distributed in an atom? The electron cloud model provides a useful visualization of how electrons are lost (oxidation) and gained (reduction) in redox reactions. Developed by Erwin Schrödinger in the 1920s, this model describes electrons as distributed within regions of probability around the central nucleus. The electron cloud model is in contrast with Bohr’s atomic model, which depicted electrons in fixed, concentric orbits around the nucleus like satellites around the Earth or cabins on a Ferris wheel. For more information on the Bohr model, see our guide on nuclear reactions.
The electron cloud model, which is the preferred model among modern scientists, emphasizes the indistinct nature of electron distribution. It proposes that electrons do not move in static orbits at specific, discrete distances from the nucleus. Instead, their locations are described by regions of probability, known as electron clouds, where an electron is likely to be found. These probabilistic regions can be visualized and illustrated as various shapes, leading to the atomic theory of subshells and electron orbitals.
----
Part 3: Molecular structure
a) Ionic bonds
The simplest type of interatomic bond is the ionic bond. Ionic bonds form when two atoms with significantly different electronegativities interact. Due to this difference, one atom donates electrons to the other, resulting in the formation of a positively charged ion (cation) and a negatively charged ion (anion). These oppositely charged ions attract each other, creating an ionic bond.
Because ionic bonds rely on differing electronegativities, the elements involved typically have very different properties. Ionic bonds usually occur between a metal and a nonmetal. For example, sodium chloride (NaCl) is a compound held together by an ionic bond. Sodium, a highly reactive metal, and chlorine, a highly reactive gas, combine to form table salt, a substance we use every day.
FIGURE 7: A SODIUM ATOM AND A CHLORIDE ION FORM AN IONIC BOND TO CREATE TABLE SALT
b) Covalent bonds
The second type of interatomic bond is the covalent bond. Covalent bonds typically form between two atoms with similar electronegativities, usually involving nonmetals or metalloids. Because these atoms have similar electronegativities, they do not donate electrons to each other; instead, they share electrons. This sharing can be either equal or unequal, depending on the difference in electronegativity between the atoms. A greater difference in electronegativity results in a bond with more partial ionic character, making it more similar to an ionic bond.
For example, a water molecule (H2O) is held together by covalent bonds. Oxygen has a higher electronegativity than hydrogen, so it attracts electrons more strongly. Consequently, the electrons are shared unequally between the oxygen atom and the two hydrogen atoms, resulting in a directional, or polar, bond. Thus, water contains polar covalent bonds.
The polarity of a covalent bond is characterized by a dipole moment, which can be calculated using the following equation:
p = dipole moment
q = net charge
d = distance between the partial charges
This equation bears resemblance to another law, Coulomb’s law, which explains the attractive force between two charged particles. In this context, the dipole moment represents a similar quantity. A large dipole moment indicates greater polarity or a larger difference in electron distribution between partial charges.
In contrast to polar molecules, elemental oxygen (chemical formula: O2) is held together by a nonpolar covalent bond. Both oxygen atoms in the molecule have identical electronegativities, preventing one atom from pulling electrons closer to itself. Therefore, the electrons are shared equally.
Lewis structures are a widely used method for depicting covalent bonds. In Lewis dot structures, electrons in the valence orbitals are represented by a dot placed next to each atom’s elemental symbol.
To construct a Lewis dot structure, start by writing the elemental symbol of the atom you are focusing on. Next, determine the number of valence electrons in its s and p orbitals. Once you have this number, place one dot above the elemental symbol. Continue placing dots in a clockwise direction around the symbol until the total number of dots equals the number of valence electrons. Repeat this process for each element involved in the covalent bond.
After illustrating each atom participating in the covalent bond, connect the electrons involved in sigma bonds with a line.
----
Gain instant access to the most digestible and comprehensive DAT content resources available. Subscribe today to lock in the current investments, which will be increasing in the future for new subscribers.